Το 17ο αιώνα, στο βιβλίο του «Dialogues Concerning Two New Sciences, 1638»
ο Γαλιλαίος έθεσε ένα πρόβλημα που αναφέρεται στην ισόχρονη κίνηση μικρών σφαιρών που έχουν ως αφετηρία σημεία μιας κατακόρυφης περιφέρειας όπως στο σχήμα.
Η πρώτη σφαίρα αφήνεται να πέσει ελεύθερα κατά μήκος μιας διαμέτρου και οι άλλες τρεις αφήνονται από σημεία της περιφέρειας και κινούνται πάνω σε τρεις χορδές - κεκλιμένα επίπεδα με κοινό σημείο το Ο. Σε κάθε περίπτωση οι τριβές θεωρούνται αμελητέες. Με τις γνώσεις Φυσικής Α’ Λυκείου μπορεί να αποδειχθεί ότι και οι τέσσερις μικρές σφαίρες φθάνουν ταυτόχρονα στο κατώτερο σημείο του κύκλου (βλέπε στο παλιό μου site
http://dapontes.gr/index.php?option=com_content&task=view&id=70&Itemid=46για ένα animation με τις 4 μικρές σφαίρες).
Το πρόβλημα στο περιβάλλον του ScratchΜε βάση τα παραπάνω πώς να φτιάξω μια απλή προσομοίωση του φαινομένου με τέσσερα μικρά αυτοκινητάκια όπως στο σχήμα;
Α.Την πρώτη φορά που προσπάθησα (2009) έφτιαξα ένα απλό project με
προκαθορισμένες τις αρχικές θέσεις των τριών αυτοκινήτων-κινητώνκαι το ανάρτησα στο Scratch website
http://scratch.mit.edu/projects/747580/με τίτλο «Isochrone problem».
Με κλικ στο κουμπί startξεκινάει η προσομοίωση: τα τέσσερα κινητά φτάνουν ταυτόχρονα στο κατώτερο σημείο του κύκλου.
Scratch applet 1
Ένα remix έφτιαξε ο χρήστης με ψευδώνυμο ahaanomegas και μπορείτε να το δείτε στη διεύθυνση
http://scratch.mit.edu/projects/748981/ .
Β. Σήμερα (2014), επαναλαμβάνω το ίδιο «ψηφιακό πείραμα» με κάποιες σημαντικές τροποποιήσεις. Αυτή τη φορά σκέφτηκα όχι μόνο να αξιοποιήσω τις δυνατότητες του
Scratch 2.0.αλλά και να δώσω στο project αλληλεπιδραστικότητα (interactivity). Χρησιμοποίησα δύο αυτοκινητάκια που κινούνται στις χορδές-κεκλιμένα επίπεδα και μια μπάλα που πέφτει ελεύθερα.
Τώρα, μπορούμε να αλλάζουμε την ακτίνα του κατακόρυφου κύκλου (με το μεταβολέα-slider R) και την επιτάχυνση της βαρύτητας (με το μεταβολέα g) καθώς και τις αρχικές θέσεις των κινητών-αυτοκινήτων (με κλικ και σύρσιμο των κόκκινων κύκλων πάνω στην περιφέρεια).
Με πάτημα του πλήκτρου ΚΕΝΟ (spacebar) ξεκινάει η κίνηση των τριών αντικειμένων και
μας προσφέρεται η δυνατότητα να παρακολουθούμε τις τιμές των επιταχύνσεων a1, a2 των δύο κινητών-αυτοκινήτων όπως και των ταχυτήτων τους v1 και v2 αντίστοιχα.
Σε κάθε περίπτωση και τα τρία κινητά φτάνουν στο σημείο 0 την ίδια χρονική στιγμή. Το project αναρτήθηκε στο Scratch Website
http://scratch.mit.edu/projects/23987786/ με τίτλο «Galileo’s Isochrone problem - 1638»
Scratch applet 2
Ο προγραμματισμός στο Scratch (scripting)Όλα ξεκινάνε με τον ορισμό των αντικειμένων-objects (σημεία ή αντικείμενα) αφού προηγουμένως γίνει μια ανάλυση του φυσικού φαινομένου και καταλήξουμε, έστω και προσωρινά, σε ένα σενάριο γεγονότων, καταστάσεων, δράσεων κ.α.
Το αντικείμενο με όνομα help οικοδομήθηκε με σκοπό να σχεδιάζονται με δυναμικό τρόπο:
---- ο μεταβλητός κύκλος ακτίνας R
---- οι χορδές Α10 και Α20
Στον κώδικα χρειάστηκε να φτιάξω δύο blocks:
CIRCLE x0 y0 R και
LINE x1 y1 x2 y2
Το αντικείμενο με όνομα Α1 αποτελεί το μεταβλητό άκρο της χορδής (ανώτερο σημείο του κεκλιμένου επιπέδου Α10 ) και είναι η αφετηρία της κίνησης του ενός αυτοκινήτου. Με σύρσιμο του Α1 πάνω στον κύκλο αλλάζω τη θέση του και επομένως αλλάζω την αρχική θέση του αυτοκινήτου.
Παρόμοιο είναι και το scripting του αντικειμένου Α2 που συνδέεται με το αυτοκίνητο 2.
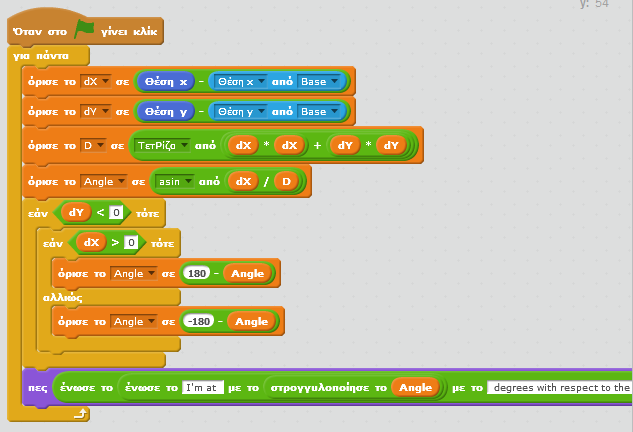
Το ενδιαφέρον επικεντρώνεται στον κώδικα κίνησης των αυτοκινήτων. Για το πρώτο αυτοκίνητο θα χρειαστεί να τοποθετείται πάντα στη θέση του σημείου-αντικειμένου Α1 και να υπολογίζεται η επιτάχυνση της κίνησης του στο κεκλιμένο επίπεδο Α10.
Παρόμοιο είναι και το scripting για την ομαλά επιταχυνόμενη κίνηση του δεύτερου αυτοκινήτου. Όσον αφορά την κίνηση της μπάλας αυτή είναι ομαλά επιταχυνόμενη με επιτάχυνση g.
….Κάποιες σκέψεις Από τον προγραμματισμό τόσο της σχεδίασης του σκηνικού, σύμφωνα με το πρόβλημα που έθεσε ο Γαλιλαίος, όσο και της κίνησης των τριών κινητών γίνεται φανερό ότι ο προγραμματιστής οφείλει να σκεφτεί όλες τις παραμέτρους του προβλήματος. Κάτι τέτοιο ξεπερνάει την επίλυση του προβλήματος στο παραδοσιακό περιβάλλον χαρτί-μολύβι. Επιπλέον, το πιο σημαντικό κατά τη γνώμη μου, είναι η δυνατότητα ελέγχου των συλλογισμών μας κατά τη διάρκεια της επίλυσης του προβλήματος μαζί με τις ικανότητες που αποκτούνται μέσα από την
ΠΑΡΑΓΩΓΗ ενός ΕΡΓΟΥ. Η ενασχόληση των μαθητών με θέματα από την ιστορία των επιστημών καθώς και η οικοδόμηση ενός προγράμματος, όπως αυτό που παρουσιάστηκε, θα μπορούσε να αποτελέσει θέμα ενός project μιας ομάδας μαθητών στο πλαίσιο του μαθήματος Φυσικής Α’ Λυκείου και η παρουσίαση του στην τάξη.
Σκοπός της διδασκαλίας της Φυσικής δεν μπορεί να είναι αποκλειστικά η ενασχόληση μόνο με ζητήματα και διαδικασίες που στοχεύουν στην επιτυχία των μαθητών στις καθιερωμένες πανελλήνιες εξετάσεις δηλαδή η επίλυση προβλημάτων συγκεκριμένου τύπου. Πρώτιστο καθήκον της διδασκαλίας δεν πρέπει να είναι άλλος από την ευρύτερη καλλιέργεια των μαθητών και αυτό είναι κάτι που τελικά επαφίεται στο διδάσκοντα.
Χρήσιμες συνδέσεις http://www.ganino.com/dialogues_concerning_two_new_sciences_by_galileo_galilei_third_day Μετάφραση του βιβλίου του Γαλιλαίου στα Αγγλικά (αφιερωμένο στην «Τρίτη ημέρα»).
daponte@sch.gr www.makolas.blogspot.gr www.dapontesgr.blogspot.gr www.dapontes.gr http://scratch.mit.edu/users/dapontes/ http://scratch.mit.edu/users/dapontesgr/